
| DE / INT: | +49 - (0)36453 - 744-0 | US: | +1 707 4810216 |
| info@layertec.de | ussales@layertec.com |
Dielektrische Beschichtungen
Durch optische Beschichtungen kann Einfluss auf die Reflektivität von Oberflächen genommen werden. Abhängig von den verwendeten Schichtmaterialien unterscheiden wir grundsätzlich zwischen metallischen und dielektrischen Beschichtungen. Metallische Beschichtungen aus z.B. Silber oder Aluminium finden Verwendung in Reflektoren und Neutralfiltern. Die mögliche Reflektivität, welche erreicht werden kann, wird durch die physikalischen Eigenschaften des verwendeten Metalls bestimmt. Eine übersicht der gebräuchlichsten Metalle finden Sie in unserem Katalog.
Durch dielektrische Beschichtungen können genau definierte optische Interferenzen zwischen den reflektierten bzw. transmittierten Teilstrahlen des einfallenden Lichts hervorgerufen werden. So kann das einfallende Licht nahezu beliebig in Transmission und Reflexion eingestellt werden.
Eine weitere Besonderheit besteht darin, dass viele dielektrische Schichtmaterialien eine sehr geringe Absorption aufweisen. So können für einen bestimmten Wellenlängenbereich Reflektivitäten bis nahe 100% (Low-Loss-Spiegel mit z.B. R > 99.999%) erreicht werden.
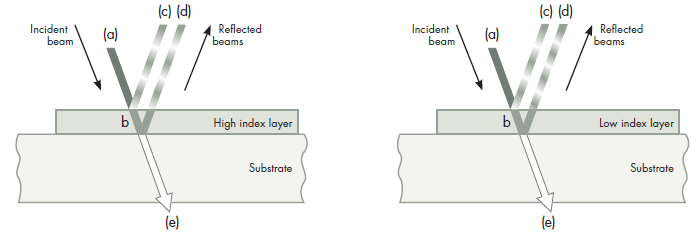
Die Lichtausbreitung in einem Substrat mit einer einzelnen dielektrischen Schicht ist schematisch in Bild 1 dargestellt. Der einfallende Strahl (a) wird an der Luft-Schicht-Grenze in einen transmittierten (b) und einen reflektierten (c) Strahl aufgeteilt. Der transmittierte Strahl (b) erfährt an der Schicht-Substrat-Grenze abermals die Aufspaltung in einen reflektierten (d) und einen transmittierten (e) Strahl. Die beiden reflektierten Strahlen (c) und (d) besitzen für jede einzelne Wellenlänge die gleiche Richtung und eine feste Phasenbeziehung. Es tritt eine Interferenz auf, in der sich die Summe von (c) und (d) abschwächen oder verstärken kann. Da bei Vernachlässigung der Absorption für die Intensitäten die Gleichung a = (c + d) + e gilt, wirkt sich die Intensität der Summe c + d auch auf die Transmission (e) aus.
Die Amplitude der Lichtwelle ist in Bild 1 durch die Schattierung des reflektierten Strahls dargestellt. Abhänging von der Phasenverschiebung der reflektierten Strahlen ergibt sich das Verhältnis von Reflexion und Transmission.
Die Phasenverschiebung der beiden Strahlen (c) und (d) wird in diesem Fall durch die optische Dicke n * d (das Produkt Brechungsindex n und der geometrischen Dicke d) der Schicht bestimmt. Dabei darf der Phasensprung bei Reflexion am optisch dichteren Medium nicht vergessen werden.
Im hier gezeigten Beispiel (Bild 1) würden sich die Strahlen (c) und (d) im linken Bild aufgrund ihrer Phasenlage verstärken, so dass die Reflexion erhöht wird und die Transmission verringert. Im rechten Bild liegt der entgegengesetzte Fall vor.
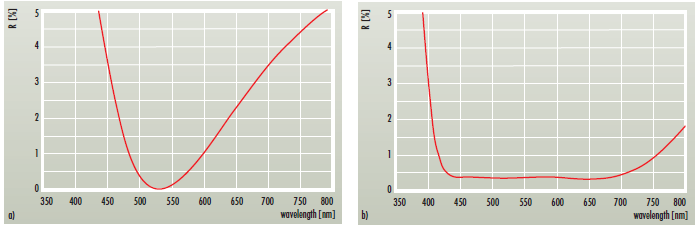
Das einfachste und gebräuchlichste Beispiel für eine Entspiegelungs-Beschichtung besteht aus einer einzelnen Schicht. Zur Entspiegelung von Glas (n=1,4) Das traditionell gebräuchlichste Material für diesen Zweck ist Magnesiumfluorid aufgrund seines niedrigen Brechungsindex von n = 1.38 im VIS und NIR. Dieses Material (mit der richtigen Dicke) reduziert die Reflektivität der Oberfläche für Quarzglas auf R∼1.8% und für Saphir auf nahezu 0%.
Einfache Antireflektionsbeschichtungen, bestehend aus 2 bis 3 Schichten, können für alle Substratmaterialien konstruiert werden.
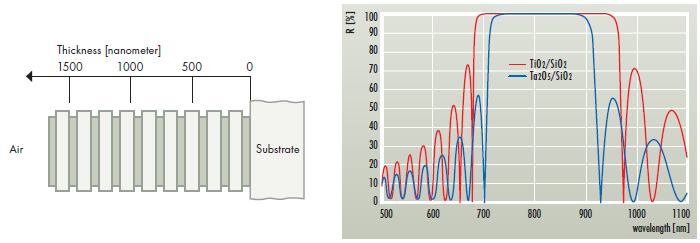
Rechts: Das Reflexions-Spektrum eines λ / 4-Systems bestehend aus 15 Schichten Ta2O5 / SiO2 oder TiO2 / SiO2
Das einfachste und gebräuchlichste Spiegeldesign besteht aus einer Reihe sich abwechselnder Lambda-Viertel-Schichten eines hoch- bzw. niedrigbrechenden Materials (n·d = λ/4), bezogen auf die Designwellenlänge. Aus diesem System folgt eine konstruktive Interferenz der reflektierten Strahlen, welche an den übergängen der einzelnen Schichten entstehen. Die spektrale Breite des Reflexionsbandes und die erzielbare Reflektivität für eine gegebene Anzahl an Schichtpaaren hängt vom Verhältnis der Brechungsindizes der Schichtmaterialien ab. Ein großes Brechungsindexverhältnis führt zu einem breiten Reflexionsband, während die Verwendung von Materialien mit einem kleinen Brechungsindexverhältnis zu einem schmalen Reflexionsband führt.
Um den Effekt unterschiedlicher Brechungsindizes zu verdeutlichen werden in Bild 3 die Reflektivitätsspektren von λ/4-Systemen verglichen. Dabei handelt es sich um jeweils 15 Schichten aus Ta2O5/SiO2 und TiO2/SiO2 bei einer Designwellenlänge von 800nm (n1/n2 = 2.1 / 1.46 bzw. 2.35 / 1.46).
Unter Annahme idealer Schichten, die weder absorbieren noch Streulicht erzeugen, nähert sich die Reflektivität mit wachsender Anzahl an Schichten ihrem Maxmimum von R = 100%.
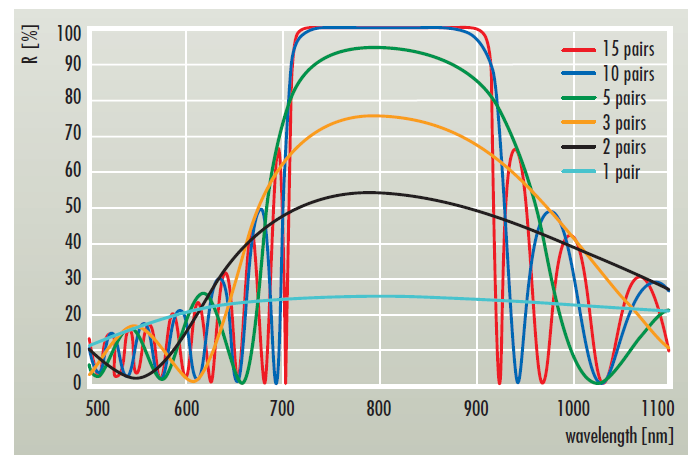
Mit einer bestimmten Zahl von Schichten können ebenso partielle Reflektoren mit genau eingestellten Reflektivitätswerten zwischen R = 0% und R = 100% hergestellt werden (Siehe Bild 4). Weicht man von der λ/4-Regel ab, so kann die Reflektivität auf jeden gewünschten Wert hin optimiert werden.
Mit wachsender Anzahl von Schichten verändert sich das Reflexionsspektrum. Dies ist besonders für Kantenfilter, wie auch für Spiegel mit weich auslaufenden Seitenbändern wichtig. Sehr steile Kanten bedingen eine hohe Anzahl an Schichtpaaren, was gleichzeitig zu einer sehr hohen Reflektivität führt.
