
| DE / INT: | +49 - (0)36453 - 744-0 | US: | +1 707 4810216 |
| info@layertec.de | ussales@layertec.com |
Components for Femtosecond Lasers
Introduction to Femtosecond Laser Optics
Short pulse lasers are used in numerous applications such as time resolved spectroscopy, precision material processing and large bandwidth telecommunication. Driven by these applications, recent developments in this field are directed to lasers generating higher output power and shorter pulses. Nowadays most of the work in short pulse physics is done with Ti:Sapphire lasers, but also dye lasers and solid state lasers on the basis of other transition metal or rare earth metal doped crystals such as Yb:KGW are used for the generation of femtosecond pulses. The reproducible generation of sub-100 fs-pulses is closely connected with the development of broadband low loss dispersive delay lines consisting of prism or grating pairs or of dispersive multilayer reflectors.
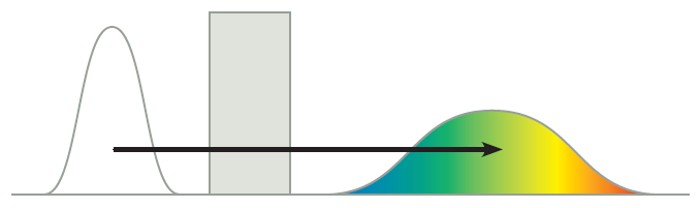
A similar broadening can be observed if a pulse is reflected by a dielectric mirror and the bandwidth of the pulse is larger or equal to the width of the reflection band of the mirror. Also broadband mirrors consisting of a double stack system cause pulse broadening, because the path lengths of the spectral components of the pulse are extremely different in these coatings.
In the sub-100 fs-regime it is essential to control the phase properties of each optical element over the extremely wide bandwidth of the fs-laser. This holds not only for the stretcher and compressor units, but also for the cavity mirrors, output couplers and the beam propagation system. In addition to the power spectrum, i.e. reflectance or transmittance, also the phase relationship among the Fourier components of the pulse must be preserved in order to avoid broadening or distortion of the pulse.
LAYERTEC offers femtosecond laser optics with different bandwidths. This catalog shows e.g. optics for the wavelengths range of the Ti:Sapphire laser in three chapters, each representing a characteristic bandwidth of the optics: standard components with a bandwidth of about 120 nm, broadband components (bandwidth about 300 nm) and ultra broadband components (bandwidth of one octave or more). Each of these chapters shows low dispersion laser and turning mirrors, negative dispersion mirrors or mirror pairs, output couplers and beam splitters of the corresponding bandwidth. Moreover, we want to present silver mirrors for fs applications which are the components with the broadest low-GDD wavelength region available.
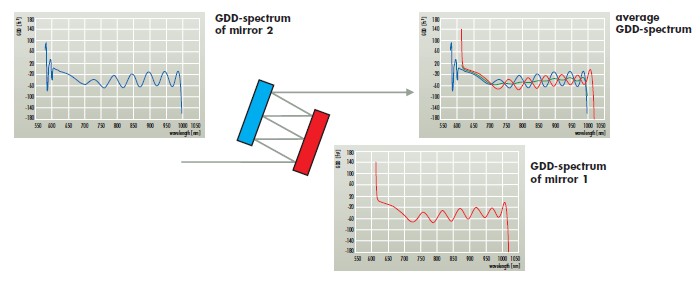
Please note that the GDD spectrum of a dielectric negative dispersion mirror is not a continuous flat graph. All types of negative dispersion mirrors exhibit oscillations in the GDD spectrum. These oscillations are small for standard bandwidths. However, broadband and ultra broadband negative dispersion mirrors exhibit strong GDD oscillations. A considerable flattening of these oscillations can be achieved by using mirror pairs consisting of mirrors with slightly shifted GDD oscillations which compensate each other. These mirror pairs are especially designed for this compensation behaviour. Figure 3 shows a schematic drawing of such a mirror pair and the corresponding GDD spectra.
If a pulse is reflected by a dielectric mirror, i.e. a stack of alternating high and low refractive index layers, there will be a phase shift between the original and the reflected pulse resulting from the time which it takes the different Fourier components of the pulse to pass through the layer system of the mirror. In general, the phase shift Φ(ω) near the centre frequency ω0 may be expanded in a Taylor series for frequencies near ω0:
The derivatives are, respectively, the Group Delay (GD) Φ´(ω0), the Group Delay Dispersion (GDD) Φ´´(ω0) and the Third Order Dispersion (TOD) Φ′′′(ω0). More strictly speaking, this expansion is only useful in an exactly soluble model, for the propagation of a transform limited Gaussian pulse and for pure phase dispersion. For extremely short pulses and combinations of amplitude and phase dispersion numerical calculations may be necessary. Nevertheless, this expansion shows clearly the physical meaning of the single terms:
Assuming the phase shift is linear in frequency (i.e. GD ≠ 0, GDD = 0 and TOD = 0 over the pulse bandwidth), the reflected pulse is delayed in time by the constant group delay and, of course, scaled by the amplitude of reflectance R. The pulse spectrum will remain undistorted.
If GDD ≠ 0, two important effect are observed:
- The reflected pulse is temporarily broadened. This broadening effect depends only on the absolute value of the GDD. LAYERTEC offers “low GDD mirrors”, i.e. mirrors with |GDD|< 20 fs2 over a given wavelength range, which are needed to preserve the pulse shape when the pulse is reflected by these mirrors.
- Moreover, the pulse becomes “chirped”, i. e. it changes its momentary frequency during the pulse time. This effect depends on the sign of the GDD, so that the momentary frequency may become higher (up-chirp, GDD > 0) or lower (down-chirp, GDD < 0). This allows to compensate positive GDD effects of nonlinear optical elements by using negative GDD mirrors.
It is also possible to use negative dispersion mirrors with high values of negative GDD for pulse compression. These so called Gires-Tournois-Interferometer (GTI)-mirrors are successfully used in Ti:Sapphire lasers, Yb:YAG and Yb:KGW oscillators and Er:Fibre lasers. Pulse compression in Yb:YAG and Yb:KGW oscillators provides pulses of some hundred femtoseconds pulse length.
LAYERTEC has own capabilities for design calculation and also for GDD measurements in the wavelength range from 250 – 1700 nm.
| References: |
| H. Holzwarth, M. Zimmermann, Th. Udem, T.W. Hänsch, P. Russbüldt, K. Gäbel, R. Poprawe, J.C. Knight, W.J. Wadsworth and P.St.J. Russell: Optics Letters; Vol. 26; No. 17 (2001); p. 1376–1378 |
| Y.-S. Lim, H.-S. Jeon, Y.-C. Noh, K.-J. Yee, D.S. Kim, J.-H. Lee, J.-S. Chang, J.-D. Park: Journal of the Korean Physical Society; Vol. 40; No. 5 (2002); p. 837–843 |
| G. Tempea, V. Yakovlev and F. Krausz: “Interference coatings for Ultrafast Optics” in N. Kaiser, H.K. Pulker (eds.): “Optical Interference Coatings”; Springer-Verlag Berlin Heidelberg (2003); p. 393–422 and the references therein |
